I’m using the NXP FRDM-K64F board in several projects: it is reasonably prices, has USB, Ethernet, micro SD card socket and connectors for Bluetooth classic and Nordic Semiconductor nRF24L01+ 2.4 GHz transceiver:
But one issue I have faced several times is that the board works fine while debugging and connected and powered by a host machine, but does not startup sometimes if powered by a battery or started without a debugger attached. I have found that the EzPort on the microcontroller is causing startup issues.
The EzPort is a special serial interface present on some NXP/Freescale Kinetis (e.g. K64F), ColdFire+ and ColdFire V2 devices. Through that port I could program the device with an SPI compatible interface: one use case is to use it instead of the normal debug interface to program the microcontroller e.g. from another microcontroller (see this link). I have not used EzPort for my projects, but I have found that this feature can cause issues if not handled properly.
The issue is that if the EzPort chip select (EZP_CS) is LOW during reset of the microcontroller, it enters the special EzPort mode. The problem is that a pull-up on the EZP_CS line might not pulled up fast enough due capacitance on the line:
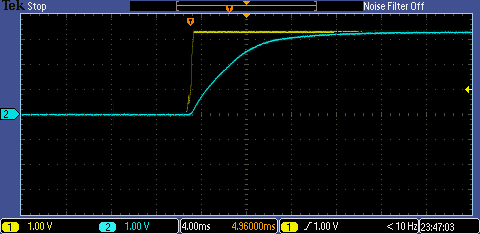
Reset and EZP_CS during Power On (Source: https://community.nxp.com/thread/332195)
The yellow signal is the reset line, and the purple one is the EZP_CS: it does not raise fast enough, therefore the microcontroller will enter the EzPort special mode during power on :-(.
Disabling EzPort
As with anything else: if something is not used, disable it! So the solution is to disable the EzPort functionality. That setting is part of the FOPT (flash option register).
With Processor Expert projects there is a setting for this in the CPU component properties (EzPort operation at boot):
This configures the NV_FOPT register:
#define CPU_FLASH_CONFIG_FIELD \
/* NV_BACKKEY3: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY2: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY1: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY0: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY7: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY6: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY5: KEY=0xFF */ \
0xFFU, \
/* NV_BACKKEY4: KEY=0xFF */ \
0xFFU, \
/* NV_FPROT3: PROT=0xFF */ \
0xFFU, \
/* NV_FPROT2: PROT=0xFF */ \
0xFFU, \
/* NV_FPROT1: PROT=0xFF */ \
0xFFU, \
/* NV_FPROT0: PROT=0xFF */ \
0xFFU, \
/* NV_FSEC: KEYEN=1,MEEN=3,FSLACC=3,SEC=2 */ \
0x7EU, \
/* NV_FOPT: ??=1,??=1,??=1,??=1,??=1,??=1,EZPORT_DIS=0,LPBOOT=1 */ \
0xFDU, \
/* NV_FEPROT: EPROT=0xFF */ \
0xFFU, \
/* NV_FDPROT: DPROT=0xFF */ \
0xFFU
__attribute__ ((section (".cfmconfig"))) const uint8_t _cfm[0x10] = {CPU_FLASH_CONFIG_FIELD};
If using the Kinetis SDK, look for something like this (usually in startup*.S):
/* Flash Configuration */ .section .FlashConfig, "a" .long 0xFFFFFFFF .long 0xFFFFFFFF .long 0xFFFFFFFF .long 0xFFFFFD7E
Summary
Usual projects have the EzPort enabled. This can cause issues with the power-on sequence of the microcontroller: if the EzPort chip select pin is low during reset, the processor will enter the EzPort mode, and this might not be what is intended. The solution is to disable to set the EZPORT_DIS bit in the flash configuration register.
Happy EzPorting 🙂
Links
- KwikStik-based EzPort programmer: http://cache.freescale.com/files/microcontrollers/doc/app_note/AN4406.pdf?fpsp=1
- FRDM-K64F Booting Problem: https://community.nxp.com/thread/332195




Thanks Erich! Can you highlight *which byte* in 0xFFFFFD7E is the FOPT byte?
LikeLike
Its the one with 0xFD. It looks backwards because it’s in little-endian format.
Thanks Erich for covering this! I lost a ton of development time due to this issue years ago when Kinetis first came out. No one else seemed to be complaining. So, I thought it was only me having the issue.
LikeLike
Eric
It is not only the EzPort but also the NMI on this pin which can cause problems. Both should be disabled on the FRDM-K64F board to avoid problems with the large capacitor on the pin.
In product designs it is also advisable to avoid connecting things like inputs that are not guaranteed to be at ‘1’ on reset otherwise this is also an issue on a fresh board which hasn’t yet been programmed – if the EzPort mode is entered the SWD/JTAG won’t work and manufacturers have difficulty programming the board – they need to apply also a voltage on the pin to get to the SWD/JTAG mode which loads firmware that subsequently disables the EzPort. This is not a big deal for us developers but in production it is best to avoid anything that could complicate.
I also don’t really understand why SDK puts flash configuration in an assembler file. When Cortex came out (about 2007) ARM were boasting that this chip no longer needs assembler code as part of its advertising campaign but people still put these “daft” bits of assembler in the code so that it is assembler/compiler-dependant (none portable), difficult to find (if one doesn’t know where it is) and usually complicated to understand (some developers [also SDK programmers it seems] possibly like to make things look complicated in order to impress others of their great intelligence and protect their jobs (?)
This is the setup I use for the FRDM-K64F:
#define KINETIS_FLASH_CONFIGURATION_BACKDOOR_KEY {BACKDOOR_KEY_0, BACKDOOR_KEY_1, BACKDOOR_KEY_2, BACKDOOR_KEY_3, BACKDOOR_KEY_4, BACKDOOR_KEY_5, BACKDOOR_KEY_6, BACKDOOR_KEY_7}
#define KINETIS_FLASH_CONFIGURATION_PROGRAM_PROTECTION (0xffffffff) // PROT[24:31]:PROT[23:16]:PROT[15:8]:PROT[7:0] – no protection when all are ‘1’
#define KINETIS_FLASH_CONFIGURATION_SECURITY (FTFL_FSEC_SEC_UNSECURE | FTFL_FSEC_FSLACC_GRANTED | FTFL_FSEC_MEEN_ENABLED | FTFL_FSEC_KEYEN_ENABLED)
#define KINETIS_FLASH_CONFIGURATION_NONVOL_OPTION (FTFL_FOPT_EZPORT_DISABLED | FTFL_FOPT_LPBOOT_NORMAL | FTFL_FOPT_NMI_DISABLED) // there is a large capacitor on the NMI/EzP_CS input so these are disabled to allow it to start without requiring an NMI handler or moving to EzPort mode
This is set to a const struct
const KINETIS_FLASH_CONFIGURATION __flash_config = {
KINETIS_FLASH_CONFIGURATION_BACKDOOR_KEY,
KINETIS_FLASH_CONFIGURATION_PROGRAM_PROTECTION,
KINETIS_FLASH_CONFIGURATION_SECURITY,
KINETIS_FLASH_CONFIGURATION_NONVOL_OPTION,
};
[it just needs one linker script entry to locate it at 0x400) but is otherwise pure C and portable].
Easily readable, understandable and no need to know what each bit means and what hex value to write. Define names are fairy clear already and C-comments complete documenting for eternity.
Regards
Mark
LikeLike
Hi Mark,
thanks for the additional point about the NMI pin: good catch, I usually always have that one disabled too unless I really need it.
I cannot understand it neither why in the SDK the vector table and such configuration is handled hidden in assembly files: this all can be done in normal C files which is (as you say) portable and easier to handle.
Assembly language should only be used for things which cannot be done otherwise.
LikeLike
Pingback: Disabling NMI (Non Maskable Interrupt) Pin | MCU on Eclipse