My mantra is *not* to use any floating point data types in embedded applications, or at least to avoid them whenever possible: for most applications they are not necessary and can be replaced by fixed point operations. Not only floating point operations have numerical problems, they can lead to performance problems as in the following (simplified) example:
#define NOF 64
static uint32_t samples[NOF];
static float Fsamples[NOF];
float fZeroCurrent = 8.0;
static void ProcessSamples(void) {
int i;
for (i=0; i < NOF; i++) {
Fsamples[i] = samples[i]*3.3/4096.0 - fZeroCurrent;
}
}
ARM designed the Cortex-M4 architecture in a way it is possible to have a FPU added. For example the NXP ARM Cortex-M4 on the FRDM-K64F board has a FPU present.

The question is: how long will that function need to perform the operations?
Looking at the loop, it does
Fsamples[i] = samples[i]*3.3/4096.0 - fZeroCurrent;
which is to load a 32bit value, then perform a floating point multiplication, followed by a floating point division and floating point subtraction, then store the result back in the result array.
The NXP MCUXpresso IDE has a cool feature showing the number of CPU cycles spent (see Measuring ARM Cortex-M CPU Cycles Spent with the MCUXpresso Eclipse Registers View). So running that function (without any special optimization settings in the compiler takes:
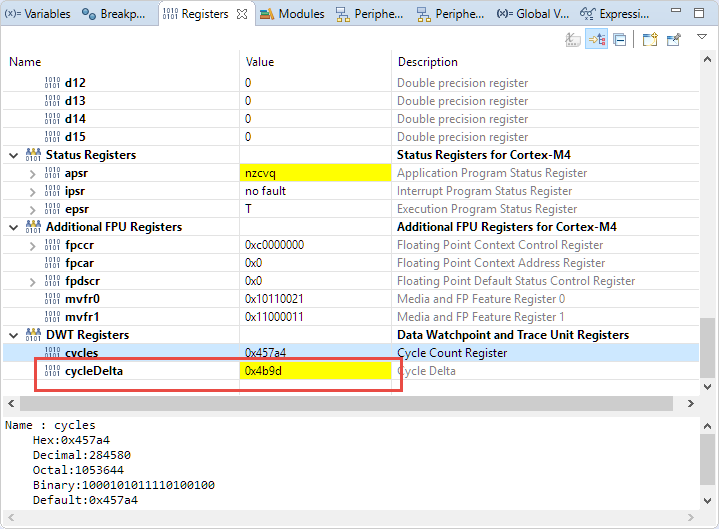
0x4b9d or 19’357 CPU cycles for the whole loop. Measuring only one iteration of the loop takes 0x12f or 303 cycles. One might wonder why it takes such a long time, as we do have a FPU?
The answer is in the assembly code: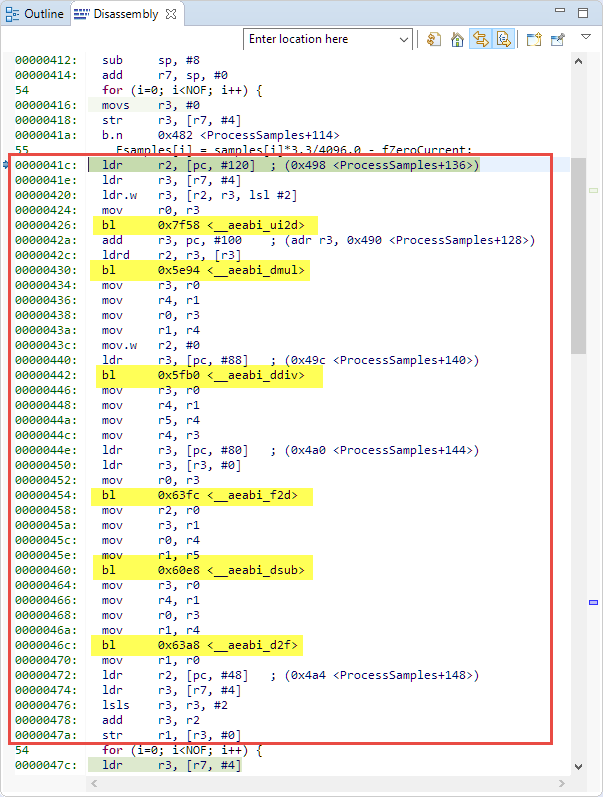
This actually shows that it does not use the FPU, but instead uses software floating point operations from the standard library?
The answer is the way the operation is written in C:
Fsamples[i] = samples[i]*3.3/4096.0 - fZeroCurrent;
We have here a uint32_t multiplied with a floating point number:
samples[i]*3.3
The thing is that a constant as ‘3.3’ in C is of type *double*. As such, the operation will first convert the uint32_t to a double, and then perform the multiplication as double operation.
Same for the division and subtraction: it will be performed as double operation:
samples[i]*3.3/4096.0
Same for the subtraction with the float variable: because the left operation result is double, it has to be performed as double operation.
samples[i]*3.3/4096.0 - fZeroCurrent
Finally the result is converted from a double to a float to store it in the array:
Fsamples[i] = samples[i]*3.3/4096.0 - fZeroCurrent;
Now the library routines called should be clear in above assembly code:
- __aeabi_ui2d: convert unsigned int to double
- __aeabi_dmul: double multiplication
- __aeabi_ddiv: double division
- __aeabi_f2d: float to double conversion
- __aeabi_dsub: double subtraction
- __aeabi_d2f: double to float conversion
But why is this done in software and not in hardware, as we have a FPU?
The answer is that the ARM Cortex-M4F has only a *single precision* (float) FPU, and not a double precision (double) FPU. As such it only can do float operations in hardware but not for double type.
The solution in this case is to use float (and not double) constants. In C the ‘f’ suffix can be used to mark constants as float:
Fsamples[i] = samples[i]*3.3f/4096.0f - fZeroCurrent;
With this, the code changes to this:
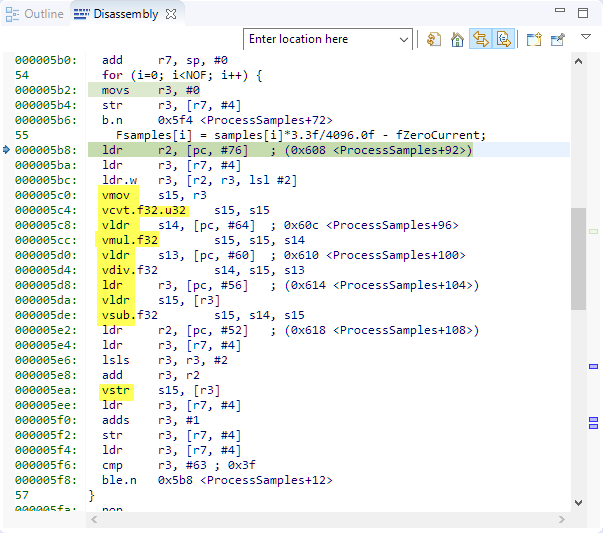
So now it is using single precision instructions of the FPU :-). Which only takes 0x30 (48) cycles for a single iteration or 0xc5a (3162) for the whole thing: 6 times faster :-).
The example can be even further optimized with:
Fsamples[i] = samples[i]*(3.3f/4096.0f) - fZeroCurrent;
Other Considerations
Using float or double is not bad per se: it all depends on how it is used and if they are really necessary. Using fixed-point arithmetic is not without issues, and standard sin/cos functions use double, so you don’t want to re-invent the wheel.
Centivalues
One way to use a float type say for a temperature value:
float temperature; /* e.g. -37.512 */
Instead, it might be a better idea to use a ‘centi-temperature’ or ‘milli’ integer variable type:
int32_t centiTemperature; /* -3751 corresponds to -37.51 */
That way, normal integer operations can be used.
Gcc Single precision Constants
The GNU gcc compiler offers to treat double constants as 3.0 as single precision constants (3.0f) using the following option:
-fsingle-precision-constant causes floating-point constants to be loaded in single precision even when this is not exact. This avoids promoting operations on single precision variables to double precision like in x + 1.0/3.0. Note that this also uses single precision constants in operations on double precision variables. This can improve performance due to less memory traffic.
See https://gcc.gnu.org/wiki/FloatingPointMath
RTOS
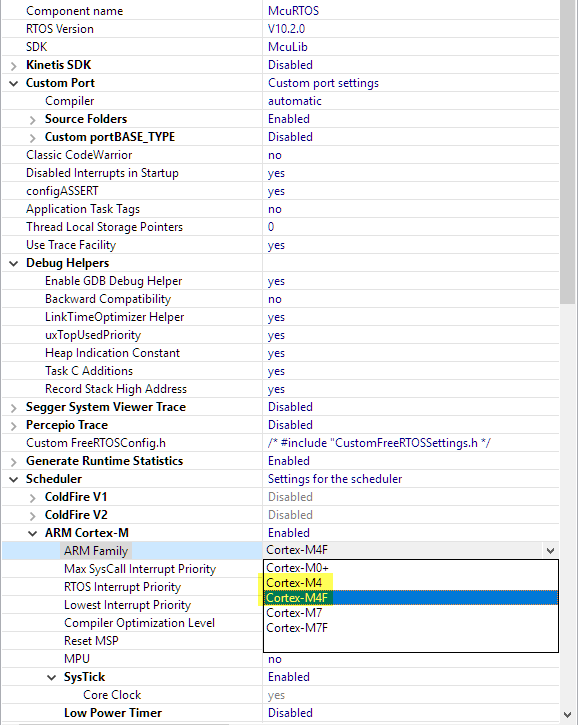
The other consideration is: if using the FPU, it means potentially stacking more registers. This is a possible performance problem for an RTOS like FreeRTOS (see https://www.freertos.org/Using-FreeRTOS-on-Cortex-A-Embedded-Processors.html). The ARM Cortex-M4 supports a ‘lacy stacking’ (see https://stackoverflow.com/questions/38614776/cortex-m4f-lazy-fpu-stacking). So if the FPU is used, it means more stacked registers. If no FPU is used, then it is better to select the M4 port in FreeRTOS:
Summary
I recommend not to use any float and double data types if not necessary. And if you have a FPU, pay attention if it is only a single precision FPU or if the hardware supports both single and double precision FPU. If having a single precision FPU only, using the ‘f’ suffix for constants and casting things to (float) can make a big difference. But keep in mind that float and double have different precision, so this might not solve every problem.
Happy Floating 🙂
PS: if in need for a double precision FPU: have a look at the ARM Cortex-M7 (e.g. First steps: ARM Cortex-M7 and FreeRTOS on NXP TWR-KV58F220M or First Steps with the NXP i.MX RT1064-EVK Board)
Links
- Measuring ARM Cortex-M CPU Cycles Spent with the MCUXpresso Eclipse Registers View
- Cycle Counting on ARM Cortex-M with DWT
- MCUXpresso IDE: http://mcuxpresso.nxp.com/ide/
- DWT Registers: http://infocenter.arm.com/help/index.jsp?topic=/com.arm.doc.ddi0439b/BABJFFGJ.html
DWT Control Register: http://infocenter.arm.com/help/index.jsp?topic=/com.arm.doc.ddi0337e/ch11s05s01.html

I reported this when I reviewed the M4 way back on the old NXP discussion board. I was a “Forum Expert” at the time (paid consultant to NXP). May need the Wayback Machine to find that post. There was also a surprise interview with me about that. It was a surprise because the interviewer told me he was doing it later and then recorded us just chatting (with me not prepared yet and not knowing it was being recorded).
My current fun and games has been with the LPC844. It would be a nice part if the documentation and header files matched the actual chip. I also found what appears to be hardware bugs in both the SCT and USART. Such is the life of an embedded programmer on a tight schedule.
LikeLike
I don’t use float, like you I prefer integer / fixed point solutions. But for those that need float, this article might be enhanced with some discussion of compiler directives … a quick look through gcc docs suggested:
LikeLike
-Wunsuffixed-float-constants
LikeLiked by 1 person
-fsingle-precision-constant
(why is the webpage making these separate comments when I paste!?)
LikeLiked by 1 person
There are flags for gcc to treat all fp constants as single precision, and single precision floating point operations take the same amount of time (single cycle) or are faster than fixed point operations (for instance when you are trying to divide 32bit fixed point values, you have to use a 64bit variable and do some black magic to get the result right and fast), you have to handle arithmetic saturation and not mentioning trigonometric functions and square roots… Floating point is just a tool (like a hammer) you have to know how to use it and when but not tell people to avoid hammers because they are evil…
LikeLike
the -fsingle-precision-constant flag indeed is very useful. And yes, in some cases using float and double is completely fine if knowing what it takes to execute things.
I agree that a full fixed point library is not an option in all cases. But using double for a sensor value which might have up to 3 digits after the dot is an overkill, as an integer data type might be used instead.
LikeLike
A 32-bit float would never be transferred to a 32-bit fixed point int. At least, I have never seen this needed. I would say your example is irrelevant since you would more than likely handle a 32-bit float as a 16-bit fixed point in which case your max size would still be 32-bit in fixed point.
LikeLike
the solution example looks like this in both Firefox and Brave browsers.
Fsamples[i] = samples[i]*3.3f/4096.0f – fZeroCurrent;
LikeLike
Yeah chrome is messed up too.
LikeLike
I can’t agree with you recommending not to use floating point arithmetics at all. Sure, there are many cases where floats should be optimized out for real-time computing. But most code (regarding LOC-count) has non-critical time constraints, even for embedded sw. This means that unconditionally eliminating floats where possible is a typical case of premature optimization.
Still a very useful example of float-limitations!
LikeLike
There are cases where indeed float and double have to be used, e.g. because the math libraries are using them. I recommend to avoid using them if possible if there are better alternatives. I see using float and double data types for things like sensor values where using an integer data type would be a better option imho.
LikeLike
I like the suggestion by Ian C to use the -Wunsuffixed-float-constants switch.
However, is there a switch for the compiler that will force floating-point operations to be done by default in single precision (vs double)?
LikeLike
The HCS08 (and HCS12) compiler had such an option to sepecify the type size of float/double. I’m not aware of such a thing for gcc.
LikeLike
The other issue here is that if HW floats are enabled, even for a single usage, then ALL push/pop stack operations will take considerably longer across the entire runtime as the register stack to be saved is considerably larger.
LikeLike
Yes, thanks for that reminder, I missed that point. The M4 can do some ‘lacy stacking’ which helps in some cases. But still, it means more work for the CPU to do a context switch because of the extra registers to save.
I have now extended the article with an extra section about this, thank you!
LikeLike
Courtesy of my upbringing back in the dark ages when clock speeds were stated in single digit MHz and forth was the answer to the question 😉
Thank you for all of the excellent work.
LikeLike
My Forth knowledge and usage are very, very minimal. I never was a fan of that language, but I know it is still in use in many older applications.
LikeLike
Shouldn’t you be using *(3.3f/4096.f) to get rid of the division (moving it to compile time)?
LikeLike
Yes, in that case the compiler can do ‘constant folding’, and this is usually how things should be written. Due the nature of floating point numbers, the result might not be the same due rounding issues, but that’s yet another danger zone using floating point numbers.
LikeLiked by 1 person
Thanks Erich!
LikeLike
You are welcome!
LikeLike
Eric
If floats are needed it is also easy to check the code in visual studio and quickly look at it in disassembled form.
Also watch out for any warnings which give hints that (unexpected and potentially time consuming conversions are taking place)
Fsamples[i] = samples[i] * 3.3 / 4096.0 – fZeroCurrent;
This compiler warning that is generated should already ring bells:
warning C4244: ‘=’: conversion from ‘double’ to ‘float’, possible loss of data
The disassembled code on a PC already looks over-complicated
00482D4D mov eax,dword ptr [i]
00482D50 mov ecx,dword ptr samples (05C85F0h)[eax*4]
00482D57 mov dword ptr [ebp-100h],ecx
00482D5D cvtsi2sd xmm0,dword ptr [ebp-100h]
00482D65 mov edx,dword ptr [ebp-100h]
00482D6B shr edx,1Fh
00482D6E addsd xmm0,mmword ptr __xmm@41f00000000000000000000000000000 (053EE70h)[edx*8]
00482D77 mulsd xmm0,mmword ptr [__real@400a666666666666 (05946E0h)]
00482D7F divsd xmm0,mmword ptr [__real@40b0000000000000 (05946F0h)]
00482D87 cvtss2sd xmm1,dword ptr [fZeroCurrent]
00482D8C subsd xmm0,xmm1
00482D90 cvtsd2ss xmm0,xmm0
00482D94 mov eax,dword ptr [i]
00482D97 movss dword ptr Fsamples (05C86F0h)[eax*4],xmm0
Consistently casting (the point of your article) helps control operations:
Fsamples[i] = (float)((float)samples[i] * (float)3.3 / (float)4096.0 – fZeroCurrent);
and this is immediately reflected in the PC’s subsequent disassembled code.
00482D4D mov eax,dword ptr [i]
00482D50 mov ecx,dword ptr samples (05C85F0h)[eax*4]
00482D57 mov dword ptr [ebp-100h],ecx
00482D5D cvtsi2sd xmm0,dword ptr [ebp-100h]
00482D65 mov edx,dword ptr [ebp-100h]
Although the VS compiler already did this optimisation (even at lowest setting), consider also
static float fConversion = (float)((double)3.3 / (double)4096.0); // get the compiler to do the calculation work [at best precision] rather than doing it at run time
..
Fsamples[i] = (float)((float)((float)samples[i] * fConversion) – fZeroCurrent);
since it may remove the (potentially high overhead) vdiv in the loop, and/or ensure optimisation is high to avoid that such calculations that need to be done just once are not “repeated” in the loop.
If highest speed is needed and you have a bit of free memory (in this particular example case) calculate the 4096 possible levels on initialisation to a look up table and then
Fsamples[i] = flook_up[samples[i]];
will fly at run time (even on a baby processor)
And yes I agree to avoiding float/double in embedded systems whenever possible – but when absolutely needed then THINK carefully about how the calculation will be performed (based on the known C rules) and keep it well under your control to avoid inefficiencies.
Regards
Mark
LikeLike
Hi Mark,
good hint about using the Visual Studio for this. And using a table instead of calculating data is always a good option for me, especially if the table can be stored in read-only memory and can be rather small.
LikeLike
When I write code that’s _supposed_ to be portable (*cough*), I’ll create a typedef, as in:
typedef mylib_float_t float
… and then carefully use mylib_float_t throughout. That way, if I ever switch to an architecture that uses native doubles, I only need to change on line of code.
LikeLike
The HCS08 (and HCS12) compiler had an option to specify if float/doubles are allowed in the code, and options to set float and/or double to either 32bit or 64bit.
I like your approach to use a typedef for floating point data types. Similar as using int32_t instead of plain ‘int’.
LikeLike
Well, at least its not like some Microchip compilers (for PIC24 etc.), where doubles are by default treated as float (unless you specify -fno-short-double). I’ve seen programmers horribly surprised by that behavior (why are my results so bad ???)…
LikeLike
I guess this is all about making benchmark look better with less code size.
LikeLike
ARM Cortex offerings made double-precision FPU an option (maybe not M0, don’t remember), which IIRC none of the early adopters took (too much power & space). Some more recent chips have double precision, for example ST32F M7 and H7 series. So for those of us the sometimes really need double a few options exist. IIRC PIC32 series had double FPU from the beginning (MIPS cores).
LikeLike
To my knowledge: M3 did not had FPU. M0: no FPU at all for cost/die size reasons. M4 had the option to have single precision FPU added by vendor, so it is an option.
M7 has single and double precision FPU by default (I believe it is not possible to remove it by the silicon vendor).
LikeLike
I have not had luck with -fsingle-precision-constant, it does not seem to do what I would expect. I am using a Kinetis K64. When I compile with that option and then set a breakpoint on a line of code that looks like this:
(float)(val)/10.0 + 233.0
If I hover over the either one of the constants, they show as “double” in the debugger.
On the other hand, If I use the “f” suffix, it works as expected and those constants show as “float”.
I know the compilier flag is doing something because I run into some issues in another unrelated part of my code, but it doesn’t seem to do what it’s supposed to do, or I’m not using the right method to confirm.
LikeLike
If you hover over the constant in the source code, then the debugger will take that *text* as an expression.
And 10.0 or 233.0 is taken as a double value (for the debugger expression).
This has nothing to do what the compiler sees as type.
It is the same as you would type ‘10.0’ in the debugger expression window, and the debugger expression parser will take this as double.
And it will take 10.0f as float.
I hope I’m able to express myself, but the thing is that the debugger expression parser is not the same as what the comiler does.
I hope this makes sense?
LikeLike
Yes that makes sense. I suppose I need to look at the assembly to confirm and not rely on the debugger parser. Thanks!
LikeLike
Why didn’t the compiler optimize out the 3.3/4096.0 and simply use the result? That removes division entirely from the equation and compilers have been optimizing like this for a long time.
LikeLike
Probably it was tested with optimisation disabled where it will presumably be done “verbose”. With optimisation enabled I would also expect the value to be a fixed const.
LikeLike
it looks like code snippet in the post is corrupted somehow. This part “for (i=0; i<NOF; i++)” doesn’t look good.
LikeLike
when I posted the copied string in the comments it looks good, but here is how it looks in the post itself: for (i=0; i & lt ; NOF; i++).
LikeLike
Thank you for pointing this out: WordPress tends to change source code to HTML code :-(. I have fixed it, so hopefully it will stay as is.
LikeLike
There is another useful gcc warning option which can help in this situation: -Wdouble-promotion. It occurs when float to double (implicit) promotion happens. It is not included with -Wall so needs
use this warning option explicitly. One more insteresting rule from C99 standard: if a function was called without prototype the float type parameters are implicitly promoted to double.
LikeLiked by 1 person
Thanks for that note! Yes, usually I do turn on this option too as it is able to flag such promotions.
As for the float-to-double promotion in C99: I believe that rule already existed in C89: if there is no prototype (a programmer error anyway), it uses the actual parameters types for the type assumption and that the function is returning an ‘int’. So if you pass 3.5 as parameter, that would be a double, but if you would use 3.5f, that would be a float type.
LikeLike
While floating point can suffer numerical issues in certain cases, I would argue that fixed point is much more susceptible to numerical issues, especially overflow, for nontrivial mathematics. Indeed, I would go further and argue that floating point is far superior to fixed point or raw integer arithmetic on most medium to high end embedded processors in terms of speed, complexity, safety, and development time. It just requires a basic understanding of what’s happening; your example should have been immediately cringeworthy to anyone who’s more than passingly familiar with floating point.
Speed:
Fixed point multiplies of 32-bit words inherently involve an intermediate conversion to a 64-bit value and a shift to bring it back to a 32-bit word. For example, if you let 0x01000000 represent unity, a.k.a. 1.0, then a multiply of 1.0 * 1.0 yields 0x0001000000000000 which then has to be shifted 24-bits to give you 0x01000000 again. Even for DSPs which have dedicated fixed point multiply instructions, this can often take several cycles. TI’s C28x core, for example, has two instructions which need to be used in conjunction with each other to do the low word and high word of the multiply and total 5 or 6 cycles. Meanwhile, almost all modern embedded FPUs will do single-cycle single precision multiplies, often with no extra latency (and non-embedded cores will often allow vectorization to do multiple flops per cycle).
On top of this, FPUs on higher end embedded processors often have instructions mapping to several standard library functions. For example, on a Cortex-M7 paired with a FPv5 FPU, fabsf(), fmaxf(), fminf(), roundf(), floorf(), ceilf(), and several other intrinsics are all single-cycle operations (although note that fmaxf() and fminf() are not supported by the FPv4 typically found with the Cortex-M4 – know your hardware). One of the most expensive parts of using an FPU (at least on Cortex-M series processors) is simply feeding the FPU with values to chew on
Safety / Complexity / Development time
A lot of numerical issues with floating point can be traced back to subtracting two similarly sized numbers – most of the information cancels out and you’re left with a few of the low-order bits. However, fixed point suffers the same issue – it’s just that fixed point always throws away the information.
Fixed point also introduces a major vulnerability, namely overflow. When doing any sort of nontrivial math, you have to consider whether the operations will overflow the representable range which means (a) having some idea of what your values are going to be a-priori and (b) normalizing values to fit nicely into the representable range.
For things like direct form II IIR filters, figuring out the dynamic range may not be too bad; it just requires some math and extra effort (thus introducing another point at which a bug can be introduced). However, for things like the covariance of an EKF, good luck; a value may vary by 5 or 8 orders of magnitude if your system goes from barely observable to very observable such that there may not even be a valid range.
As for normalization, it’s frequently necessary to deal with large differences in order of magnitude which frequently results in code that looks like this (example taken from a motor controller stack that I’ve worked on):
// vq_ffwd = w*(Ld*id + lambda)
_iq vq_ffwd_pu =
_IQmpy(_IQmpy(speed_pu, idq_cmd_pu.d),
_IQ(2.0 * MATH_PI * USER_IQ_FULL_SCALE_FREQ_Hz * USER_IQ_FULL_SCALE_CURRENT_A *
USER_MOTOR_Ls_d / USER_IQ_FULL_SCALE_VOLTAGE_V)) +
_IQmpy(speed_pu, _IQ(2.0 * MATH_PI * USER_IQ_FULL_SCALE_FREQ_Hz * USER_MOTOR_LAMBDA /
USER_IQ_FULL_SCALE_VOLTAGE_V));
Beside being almost unreadable, it’s impossible to tell if this code is correct by local inspection; you have to look up each constant and check the math operation by operation to make sure there’s no overflow. Further, when changing parameters, there’s always a risk of breaking something or inducing overflow in a corner of your operational envelope. Floating point has no such issues. Because of this, I’ve found that floating point is several times faster to develop with.
I can also go into the complexity of integer casting rules, how floating point often naturally handles exceptional situations, readability, and a bunch of other issues, but this comment is already getting too long. The big takeaway is that floating point is better as soon as you start doing nontrivial things.
LikeLiked by 1 person
Hi Nicholas,
thanks for your detailed thoughts on this. There is always a balance between simplicity and complexity, and using fixed-point vs. floating point is one good example for it. I did not advocate to use fixed-point in all cases: it always depends on the usage, and you give some good examples. However, I see lots of engineers using floating point without understanding it, and even using floating point where it is simply an overkill. Sure, if you have a powerful MCU with single and double precision FPU with lots of RAM and ROM, there is no point about thinking about optimizations. So I agree with your point, that floating point is better for non-trivial things. My point is that floating point is not needed for the trivial things :-).
LikeLike
The code in the article is misleading:
int32_t centiTemperature; /* -37512 corresponds to -37.512 */
“centi” means “hundredths”, whereas -37512 represents thousandths of -37.512, or milliTemperature rather than centiTemperature.
LikeLiked by 1 person
Hi Michael,
thanks for pointing this out. Indeed the comment is misleading, I have fixed it now.
Thanks again!
LikeLike
Great article. Hope we didn’t have to scroll to right and left to read it.
LikeLike
Thanks, and sorry about the formatting: WordPress keep to screw up code in older articles :-(. I have reformatted the article, so it should be fixed now. Thanks for reporting!
LikeLike
Hi Erich,
Can you please recommend a solution to check if in any part of the project we are using software libraries for floating point computation ? I have looked at the disassembly as explained here. However, I think its not feasible to look into each function manually to determine if hardware floating point unit is being used.
Is there a better approach, like looking at map file ? Thank you
LikeLike
What comes to my mind: Have you tried arm-none-eabi-readelf with the -A option to dump the information of the .elf/Dwarf file already?
LikeLike
Thank you Erich. I wasn’t aware of this command line option and tried the above command with -A, it didn’t display any info. However, other command line options worked ex : h, s and so on. So I think there is nothing wrong in the way I used.
One thing to note though I’m using ARM toolchain and it generates a .axf file which I believe is equivalent to .elf file from GNU tool chain. Not sure if that’s the reason for the command with -A not working. Thank you.
LikeLike
What version of readelf are you using? I’m using the following:
GNU readelf (Arm GNU Toolchain 12.3.Rel1 (Build arm-12.35)) 2.40.0.20230627
This version has the -A option
-A --arch-specific Display architecture specific information (if any)
LikeLike
I am using slightly older version.
GNU readelf (GNU Arm Embedded Toolchain 10.3-2021.10) 2.36.1.20210621
This version does have an -A option too.
I did also ask the same question in ARM forum
https://community.arm.com/support-forums/f/architectures-and-processors-forum/55650/looking-for-a-way-to-determine-if-software-libraries-are-used-for-floating-point-computation
Someone from ARM mentioned there may not be a tool for this.
LikeLike
Yes, I have not found a tool or special compiler option for it. What I use is the #pragma GCC poison with the –wrap linker option, I posted an article about it here: https://mcuoneclipse.com/2024/03/13/how-to-make-sure-no-floating-point-code-is-used/
LikeLike
Thank you Erich. I will give it a read.
LikeLiked by 1 person
Pingback: Binary, do you use hard-float or soft-float? @McuOnEclipse « Adafruit Industries – Makers, hackers, artists, designers and engineers!